
통계수업을 듣기전에 보면 아주 좋을 책이다. 이 책을 통해 배운 것은 다음과 같다.
표본의 평균과 분산을 통해 모평균을 추정할 수 있다
표본갯수가 30개 이상인 경우 중심극한정리에 따라 표본은 N(모평균,표본분산/n)인 정규분포이므로, 모평균의 신뢰구간을 구할 수 있다.
카이제곱곱분포를 통해 모분산을 추정할 수 있다
카이제곱분포는 표준정규분포 값 z를 제곱한 것들 합한 값들의 분포이다. 변수의 갯수는 곧 자유도 n이 된다. 표본데이터를 X^2로 표준화시키는 과정은 아래와 같이 나타낼 수 있다. s는 표본의 표준편차이므로 n-1을 곱해주면 편차를 제곱한 것만 남고, 모분산으로 나누어주면 이것은 z^2의 행태가 되어 카이제곱분포를 따른다.
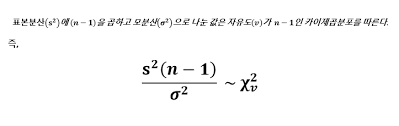
저렇게 구한 카이제곱갑을 통해서 우리는 모분산을 추정해 볼 수 있다. 카이제곱분포는 구간별 분포값이 알려져 있으므로 아래와 같은 영역에 대입해주면, 모분산의 신뢰범위를 추정해볼 수 있다.
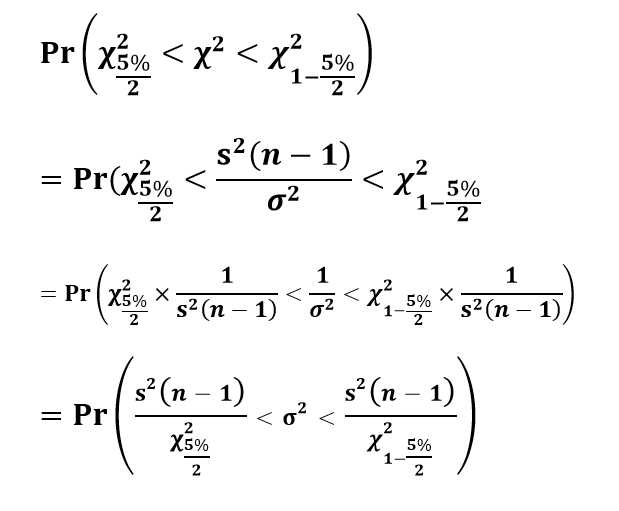
t분포를 통해 모평균을 추정할 수 있다
표본크기가 30개 이하인 경우에는 정규분포를 따르지 않아 이때는 결합분포(정규분포와 카이제곱분포의 조합)인 t분포를 쓴다. 모평균의 신뢰구간은 t분포의 확률에 따라 구할 수 있다. t분포는 모분포가 정규분포가 아닌 경우에도 사용할 수 있는 것으로 알려져 있다.
'독서 > 머신러닝' 카테고리의 다른 글
| 밑바닥부터 시작하는 딥러닝 4 (0) | 2024.09.16 |
|---|---|
| 바닥부터 배우는 강화학습 (0) | 2024.08.11 |
| 벌거벗은 통계학 (0) | 2024.05.23 |
| 통계101 데이터 분석 (0) | 2024.05.12 |
| 파이썬 라이브러리를 활용한 머신러닝 (0) | 2024.05.11 |