밑바닥부터 시작하는 딥러닝 4권. 강화학습의 기초를 설명하는 책이다. 왜 진작 밑바닥 시리즈를 읽지 않았는지 안타까움이 생길 정도로 단계적으로 이해하기 쉽게 설명하는 책이었다. 이 책을 통해서 겨우, 강화학습을 좀 이해하게 되었다.
지도학습 : 정답지로 배우는 학습
비지도 학습 : 데이터로 배우는 학습
강화학습 : '행동'과 '보상'(보상은 정답이 아니다)을 통해 trial & error로 배우는 학습. .
시간순서가 없을 때
실행횟수가 추가될 때 1/n만큼의 증분으로 표현되는 Qn의 수식을 주목하자.
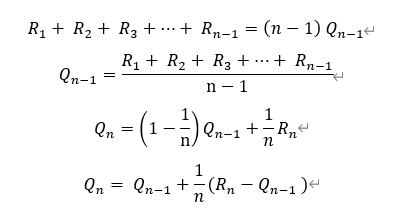
1/n을 임의의 알파로 바꿀수도 있으며, 그러면 그것은 동일가중이 아닌 기하적인 가중치를 의미하게 된다. 이것이 일반적으로 사용되는 증분형태의 가치/Q함수 수식이다.

벨만 방정식
앞에서는 시간 순서가 없었으나, 이제부터는 시간순서에 따라 오늘시점에서 미래에 영향을 끼치는 결정에 대한 판단을 하고자 한다. 오늘 시점에서 수익 G의 기대값(미래가치)는 아래와 같다.
G(t) = R(t) + r* R(t+1) + r^2* R(t+1) + r^3* R(t+1) ....
= R(t) + r* G(t+1)
이 공식이 성립하려면 오늘 이 시점에서 판단을 하려면 미래의 결정에 대한 모든 정보를 이 시점에 가지고 있어야 한다. 이것을 마코브 결정 과정(MDP)이라고 한다. 수익 G 공식과 증분형태의 가치/Q함수를 통해 벨만방정식을 도출 할 수 있다. 벨만방정식은 가치함수 V, 벨만최적방정식은 Q함수를 기반으로 한다.
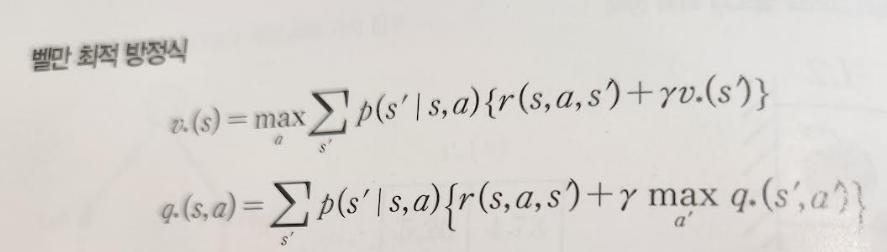
다이나믹 프로그래밍
동적프로그래밍(DP)를 통해 행동을 반복하여 초기값이던 각 state들의 가치를 업데이트 하여 최종적인 값을 찾는다. 정책반복은 모든 경우에 대해 가치를 찾은 후에 정책을 업데이트 하는 방식이며, 가치반복은 가치를 업데이트하면서 정책 업데이트도 같이 진행하는 방식이다. 따라서 가치반복이 더 빠르다.
몬테카를로법
정책반복과 가치반복은 모든 경우의 수를 알고 있고, 모두 수행할 수 있을만큼 가짓수가 제한적인 경우에만 가능하다. 하지만 일반적으로 실무에서 마주치는 문제들은 그렇지 않으며, 행동과 보상을 통한 학습은 샘플을 통해서만 가능하다. 몬테카를로법은 샘플을 통한 학습이며, 에피소드가 끝난 후에 가치를 반영하고 정책을 업데이트한다. 가치를 반영하는 방식은 state와 reward를 메모리에 쭉 저장해놓고 반대방향으로 한 state 씩 업데이트한다. 수식으로 표현하면 아래와 같다. 에피소드를 통해 업데이트되는 가치는 상태가치함수(V)가 아니라 (상태,행동) 쌍의 가치인 Q함수다.


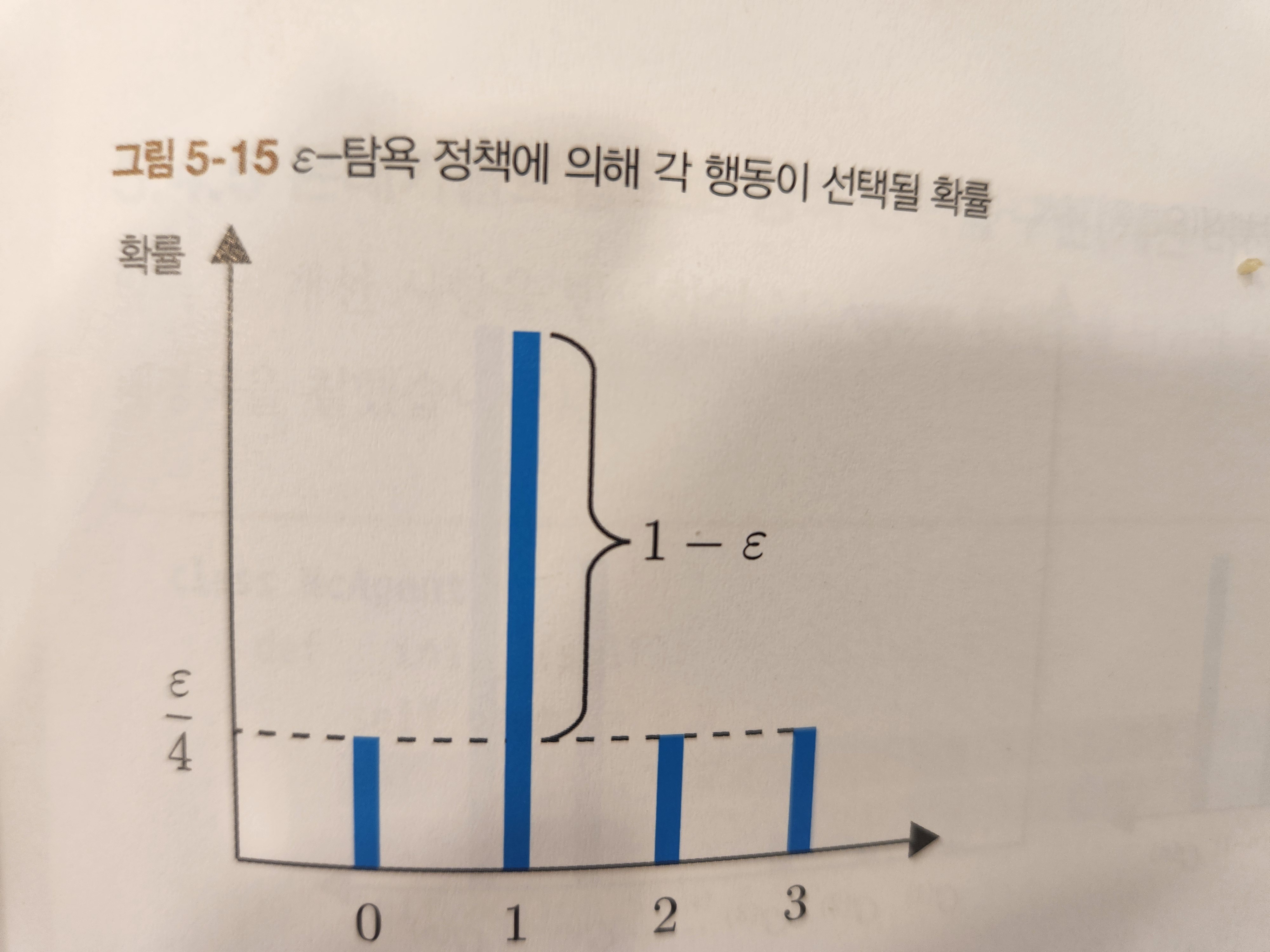
에피소드의 가치를 모두 업데이트 한 후, 정책 업데이트를 한다. 아래는 정책을 분포로 나타내는 경우인데 greedy 정책을 선택하는 경우 가장 가치가 큰 선택에 대해 1로, 나머지는 모두 0으로 업데이트 할 수 있다. 하지만 이 경우 탐색을 제한하므로 아래와 같이 가치가 낮은 경우에도 입실론/4 만큼의 확률을 부여하여 탐색의 가능성을 살려둔다. 이런 방식을 입실론-greedy 정책이라고 한다.
TD법
TD법과 몬테카를로법의 차이는 한 스텝마다 가치반영 및 정책업데이트를 수행한다는 점이다. 이는 정책반복법과 가치반복법의 차이와 유사하다.
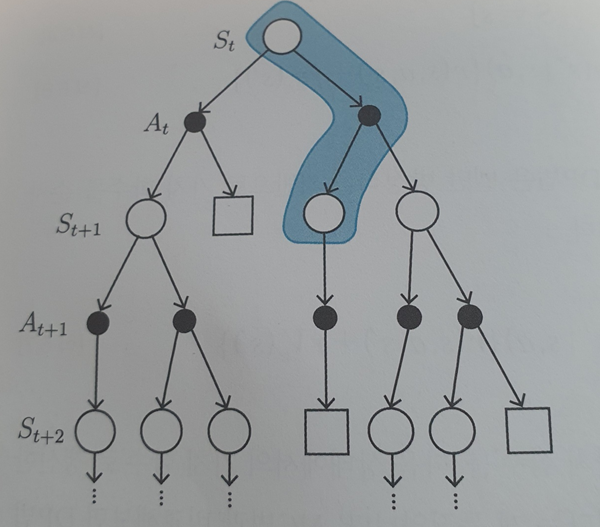
Q-learning
가치반영후 정책업데이트를 할때 정책을 target 정책과 행동정책 2가지로 나눈다. 행동정책은 학습을 위한 것이며, target 정책은 활용을 위한 정책이다.
DQN(Deep Q learning)
실제 환경에서는 행동의 경우의 수가 너무도 많은 경우가 대부분이다. 이 경우에 딥러닝을 활용하여 다양한 선택이 가능할 수 있도록 발전시킨 것이 DQN이며, 이를 통해 강화학습은 비약적인 발전을 이루었다.
'독서 > 머신러닝' 카테고리의 다른 글
| 바닥부터 배우는 강화학습 (0) | 2024.08.11 |
|---|---|
| 통계학입문 (0) | 2024.05.24 |
| 벌거벗은 통계학 (0) | 2024.05.23 |
| 통계101 데이터 분석 (0) | 2024.05.12 |
| 파이썬 라이브러리를 활용한 머신러닝 (0) | 2024.05.11 |